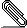
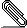
Systèmes de Cramer

Préambule

Les systèmes de Cramer sont des systèmes de n équations linéaires à n inconnues. Il ont la forme générale suivante :

On peut les représenter de façon matricielle par la formule AX=Y où A est la une matrice nxn et où X et Y sont des vecteurs colonnes à n composantes.

Si n=3, on a :

Les types matrice et vecteur

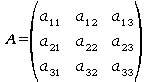
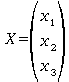
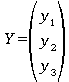
Commençons par définir une constante nMax définissant le nombre d'équations et d'inconnues du système.

 const nMax = 3;

Définissons le type vecteur comme un tableau de nombres.

 type vecteur=array[1..nMax] of Real;

Définissons le type matrice comme un tableau de nombres doublement indicé.

 type matrice=array[1..nMax,1..nMax] of Real;

1. Ecrire la procédure lireVecteur(var v:vecteur); qui permet de définir un vecteur en donnant ses composantes.
2. Ecrire la procédure lireMatrice(var m:matrice); qui permet de définir une matrice.
3. Ecrire la procédure afficheSyst(A:matrice; Y:vecteur); qui affiche le système AX=Y.
4. Ecrire la procédure afficheSol(X:vecteur); qui affiche la solution d'un système.
5. Vérification. Ecrire un programme utilisant les procédures précédentes.

Systèmes triangulaires

Nous allons résoudre un tel système en effectuant des combinaisons linéaires sur les lignes de façon à obtenir un système triangulaire supérieur, c'est à dire un système pour lequel la matrice A contient des 0 dans le triangle inférieur délimité par la diadonale principale (a_ij = 0 pour i>j ).

Si n=3, on aboutit à la matrice :

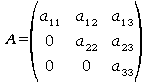
Le système devient :

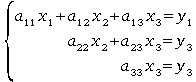
Il est alors facile à résoudre par substitution en partant de x₃.

1. Ecrire la procédure resTriangleSup(A: matrice; Y : vecteur; var X : vecteur); qui permet de résoudre le système AX=Y lorsque A est une matrice triangulaire.
2. Vérification. Définir les constantes A et Y :

   const A:matrice=((1,5,7),(0,3,4),(0,0,5));
   const Y:vecteur=(3,2,10);
   

   puis résoudre AX=Y.

Triangulation

Pour transformer tout système en système triangulaire supérieur nous utiliserons des combinaisons linéaires des lignes.

Appelons L₁, L₂, .... , L_n les différentes lignes du système. Pour faire apparaître des 0 dans la 1ère colonne, si a₁₁ est différent de 0, nous remplacerons la ligne L₂ par L₂ - (a₂₁/a₁₁)L₁, puis la ligne L₃ par L₃ - (a₃₁/a₁₁)L₁, etc...

Il suffira ensuite de reprendre le même procédé pour les colonnes suivantes en laissant la 1ère ligne et la 1ère colonne de côté.

Si a₁₁ est égal à 0, il faudra trouver une ligne dont le premier coefficient est non nul et l'échanger avec la première ligne. Si une telle ligne n'existe pas, le système n'est pas régulier (déterminant nul) et n'a donc pas une solution unique.

Pour des raisons de meilleure approximation, on a intérêt à faire en sorte que le coefficient par lequel on divise soit le plus grand possible en valeur absolu. Nous allons donc toujours commencer par rechercher le plus grand coefficient (en valeur absolue) sur une colonne pour le placer en première ligne.

Si ce coefficient est nul, le système n'est pas régulier. Pour tenir compte des arrondis, nous considèrerons comme nul les coefficients inférieurs à 10^-8 en valeur absolue.

1. Ecrire la procédure gaussPartiel(A : matrice; Y : vecteur; var X : vecteur); qui commence par transformer le système AX=Y pour le rendre triangulaire, puis calcule la solution en utilisant la procédure resTriangleSup vue précédemment.
2. Ecrire un programme permettant d'entrer un système d'équation et de le résoudre.